Let N ∼ Poisson(λ). You flip a coin a random number of times N. Each time a head will come with probability p, independently of N. Let X be the (random!) number of heads outcomes and Y be the (also random) number of tails. Find the distribution of X and Y . Hint: Conditioning on the value of N, the number of heads is a binomial random variable. Use the total probability theorem to conclude.
ANSWER
Here by the problem,
Now we flip a coin a random number N where each time a head will come with probability p ( and a tail will come with probability (1-p) , independently of N.
So here we assume X be the number of heads and Y =N-X be the number of tail.
Clearly we note that, X|N=n~Binomial(n,p) with pmf,
and similarly, Y|N=n~Binomial(n,1-p)
So the distribution of X (unconditional) is obtained as follows where we note that,
Now clearly as  then the lower limit of n be x , not 0.
then the lower limit of n be x , not 0.
Let us assume z=n-x then z=0,1,2,.....
So clearly, 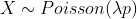
Similarly we can show  ( As Y|N=n~Binomial(n,1-p) hence just like X it is just replaced p by 1-p)
( As Y|N=n~Binomial(n,1-p) hence just like X it is just replaced p by 1-p)
Comments
Post a Comment