Data Sheet: Activity - Osmosis Name Course Date Activity Data Code Procedure I -Test Solution 1: Water Complete the tablesand questions below using your data and information found under the Background tab Data Table I Note: Difference in Final Volumes = Final Volume of Test Sol - Final Volume of Water Trial Starting Volume of Test Solution (L) Starting Volume of Water (L) Final Volume of Test Solution (L) Final Volume of Water (L) Difference in Final Volumes (L) 1 1.28 1.75 1.51 1.52 -0.01 2 1.28 2.00 1.64 1.64 0 Observations and Questions [1] Given that the final heights (and volumes) are the same for the water and test solution, what can you...

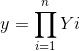
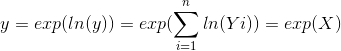

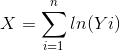
![\mu = E[Xi]](https://media.cheggcdn.com/media%2F5c1%2F5c13f0d5-1757-45ac-9857-bc69eed05969%2F23e19639-6952-4d66-bf9f-f7d729324c19.gif)
![\sigma ^{^{2}} = V[Xi]](https://media.cheggcdn.com/media%2Fefe%2Fefe14016-3141-4d72-96cf-27b29916f73f%2Ff550f675-c2a4-4c1d-ba3a-14fddca040f4.gif)
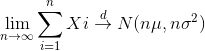
![X \xrightarrow[n\rightarrow \infty]{d } N (n\mu ,n\sigma ^{2})](https://media.cheggcdn.com/media%2F366%2F366caba8-10e5-470d-8b3a-f6c636f93e8d%2Ff624942f-99dd-4877-a6c5-f23965dc45e2.gif)
![E[X] = n\mu](https://media.cheggcdn.com/media%2Fd31%2Fd3107007-00b2-4af1-baef-e8daecf36d4f%2F20e7d089-8dd0-4902-a347-a3066a2d5639.gif)
![V[X] = \sigma{\sqrt{}}n](https://media.cheggcdn.com/media%2Fe90%2Fe907fa54-0914-48d4-9b30-9bcfb3ec06ae%2F04bbfa80-e633-4e1d-ba4f-daa67d3bc142.gif)
Comments
Post a Comment